发布于 2024-07-27 11:51:09

发现偏爱好奇的心 ——— 数学哲学原著《大数域原理》科普介绍

王强(Charlie Wang)：大连理工大学计算机系工学学士；美国爱荷华州马赫西大学计算机学院获计算机科学硕士。美国硅谷软件工程师, 工业企业应用整合专家。《大数域原理》和《Principles of Large Number Domain》等书作者。

十万个为什么 3.0 丛书

亚马迅出版的中文版《大数域原理》和英文版《Principles of Large Number Domain》是描述作者对数学发散无穷大的一系列探索发现的原创数学哲学著作。下面就对此书做一个科普介绍。

《大数域原理》旨在介绍继2019年3月第一作者在美国硅谷破解分数奥秘后, 同年七月又在中国廊坊发现分数域生成率大常数Q, 彻底破解一百多年前德国数学家希尔伯特开列的大名鼎鼎的23个世纪数学难题第一题“连续统假设”。接着一群热爱科学热爱自然的中国工程师, 教授, 专家及企业家在追求真理的信念感召下, 在为中华民族抢占人类智商制高点的强大使命感的驱动下, 在强烈好奇心和质疑挑战精神的激励下花费巨大人力物力成功验证连续统假设以及大常数Q的有趣经历。

破解连续统假设难题不是终极目的, 探索发现的真正目的是探索世界第一难题下面最底层逻辑, 探索当代哲学数学科学的天花板和边界在哪里以及它们外面的奥秘, 探索当代数学公理框架外面的未知世界, 探索大自然更深刻的规律, 探索宇宙更深层的秘密, 找到提升人类文明进阶的出路。攻克连续统假设之后, 又发现了更多比连续统假设更深奥更激动人心更惊天动地又前所未见的自然规律和宇宙奥秘。和后面的一系列原创发现相比, 破解连续统假设只能算一个盛宴大餐前的第一碟开胃小菜, 奠基未来数学万里长城的第一块砖石, 奥运大赛前初级入门的第一个热身练习, 地平线上刺破无边黑暗的第一道曙光。连续统假设除了启迪开智, 撕开无穷大的缺口, 历史使命就结束了, 后来发展基本可以忽略不计。此书分享整个跌宕起伏峰回路转波澜壮阔震撼人心的探索自然发现奥秘的惊险历程。

一、背景

先介绍一下什么是集合的基数。所谓集合的基数就是集合里基本元素的个数。每个国家的最基本的元素是人。比如美国有三亿人口, 美国人集合的基数是三亿；中国有十四亿人口, 中国人集合的人口基数是十四亿；新加坡有五百万人口, 新加坡人集合的人口基数就是五百万。一个小家A有三口人, 则小家A的人口基数是3。一个大家族B四世同堂有100人, 大家族B基数就是100，这些都是最简单的有限有界集合，其基数是我们熟悉的确定数。其他有界无限集合如区间[0，1]里面的所有分数集合，无界无限集合如整个数轴上所有整数的集合。这些集合的基数是我们陌生的无穷大。

什么是史无前例的连续统假设呢？根据维基百科，连续统假设（英语：Continuum hypothesis，简称CH）是数学中一个猜想，也是希尔伯特的23个问题的第一題, 由康托尔提出, 关于无穷集的可能大小。其为：不存在一个基数绝对大于可数集而绝对小于实数集的集合。连续统假设研究的是无穷大集合如整数，分数和实数等集合基数之间的关系。康托尔一直怀疑分数集合基数大于整数集合基数，当他用变魔法般的对角线法稀里糊涂证明了分数集合基数等于整数集合基数之后，打消了怀疑。（见图1）

图1 ：康托尔证明分数基数等于整数基数的对角线法

挡住人类进步的不是有限有界的简单集合, 是无穷大。从古至今, 无穷大一直是神秘莫测, 难以琢磨, 高不可攀的沉重的话题。纵观人类文明史, 几千年来人类在无穷大面前一直是绝望无助的。即使笛卡儿, 欧拉, 高斯, 黎曼等这样罕见的盖世天才也一筹莫展, 不知所措, 望而却步, 避之不及。

德国数学家格奥尔格·康托尔是人类历史上罕见的数学天才和英勇无畏的开拓者。一个多世纪以前, 康托尔以远超欧拉高斯黎曼的空前非凡超群绝伦的抽象力和想象力第一次在人类历史上开天辟地发现了无穷大基数, 创立了可数集的概念, 开创性提出了可以用无穷大度量无穷大的卓越思想, 用伽利略发明的一一对应映射方法计算了三大无穷大集合, 整数集合, 分数集合和实数集合的基数, 提出了三级无穷大的概念, 首次采用大名鼎鼎的对角线法证明整数集合基数等于分数集合基数, 进而提出了震撼世界的连续统假设。见图1。康托尔以一人之力开天辟地, 独创现代数学基础的传统经典无穷大理论——集合论。这是人类继发现实数, 无穷小微积分之后基础数学领域里的又一个伟大的里程碑。

无穷大这座高耸入云的高山后面, 是人类从未见过的无穷无尽的五彩缤纷壮丽秀美的全新世界。

康托尔的伟大发现揭示了无穷大这个全新世界的一角。

康托尔这些开创性的工作震撼全球, 康托尔提出的集合论和连续统假设, 更是引爆了数学史上惊天动地的第三次数学危机。数学史上群星璀璨, 天才辈出, 但是能够引发数学危机的盖世英豪却屈指可数, 如发现无理数引发第一次数学危机的希帕索斯, 发现微积分无穷小引发第二次数学危机的牛顿和莱布尼兹等都是人类历史上大名鼎鼎伟大卓越千古流芳的英雄人物。他们的丰功伟绩和辉煌成就被写进现代文明的伟大结晶的数学手册和所有国家的数学教科书, 启迪着人类的世世代代和子子孙孙。

100多年前, 康托尔对数学和对人类文明的伟大发现和开创性工作得到了上个世纪伟大数学家希尔伯特的高度赞赏和肯定。据百度百科："希尔伯特(Hilbert David, 1862.1.23-1943.2.14) 高度赞誉康托尔的集合论 '是数学天才最优秀的作品', '是人类纯粹智力活动的最高成就之一', '是这个时代所能夸耀的最巨大的工作'。在1900年第二届国际数学家大会上, 希尔伯特高度评价了康托尔工作的重要性, 并把康托尔的连续统假设列入20世纪初有待解决的23个最重要的世纪数学难题之首。

二、进展

康托尔提出的连续统假设(简称CH)是基础数学中最困难、最有争议的问题, 而大名鼎鼎享誉世界的超级数学难题, 被誉为数学皇冠上的明珠的哥德巴赫猜想和黎曼猜想仅仅名列第八。可见在学识渊博远见卓识的希尔伯特眼里, 两者在难度, 深度, 重要性和价值上完全不在一个档次。毕竟哥德巴赫猜想只是研究整数数域和质数数域的元素之间关系的一个猜想, 远没有上升到无穷大整个质数数域的层面, 更没有触动传统数学现有的基本框架和公理体系, 基数太小而局限性太大, 无法对数学进步作出开天辟地的重大贡献。上个世纪, 库尔特·哥德尔曾证明连续统问题在现有的数学框架下无解。其他数学天才也屡次冲击连续统假设这个世界头号难题, 均铩羽而归, 无功而返。一百年多过去, 无数英雄豪杰前赴后继, 连续统假设依然稳如泰山, 岿然不动。人类几乎动用了整个种群的力量, 动用了整个文明的力量, 集中了这个种群智商最高的天才大脑, 居然无法撼动这个世纪第一难题一根汗毛。

连续统假设的一个最重要的结论是整数集合(可数集)基数等于分数集合基数。即分数集合元素和整数集合元素的个数一样多。只要找到一个反例, 否定了这个结论, 连续统假设就被推翻了。过去一百多年，无数数学天才就在大海捞针，寻找这个反例，却一无所获。

一个世界顶级难题，解决方案连八字都没一撇，门都没摸着，路都不知在何方，无穷大啥模样都没有看清楚，分数来源都一塌糊涂，与此相关的两个研究居然破天荒的两次获颁有数学界诺贝尔奖之称的菲尔兹奖，奖励哥德尔和科恩为无穷大探索作出的辛苦付出，连续统假设的重要性可见一斑。

自康托尔创立经典无穷大理论, 希尔伯特开列23个世纪数学难题100多年以来, 人类文明先后步入电气文明, 核能文明, 信息文明, 取得了翻天覆地的伟大进步, 但是遗憾的是我们在最重要的基础数学理论方面, 在康托尔开辟的无穷大领域, 竟无尺寸之功, 原地踏步, 进展为0, 整个种群的几乎所有精英一直在忙忙碌碌低端低含金量低价值的大量琐碎重复性的鸡毛蒜皮边边角角零零碎碎的东西却一直自娱自乐认为在做着什么了不起的伟大事业。近百年来, 人类在基础数学和基础科学没有获得任何可以媲美开普勒, 笛卡儿, 牛顿, 莱布尼兹，法拉第和爱因斯坦级别的框架性, 体系性和完整世界观根本转换档次的革命性重大突破和发现。人们一直怀疑地球文明是不是被宇宙深处某个更发达更高等文明锁死了, 被什么看不见摸不着的怪物堵住了去路, 似乎总有个什么厚厚的玻璃天花板罩在我们头顶的上方无法突破, 却始终看不见摸不着也不知道这个天花板在哪里。这个前进道路上看不见摸不着却又似乎无处不在的神秘怪物, 高天上似乎存在又似乎不存在的厚厚天花板就是无穷大。发散无穷大这个难以逾越的障碍挡住了所有数学天才前进的脚步, 也堵死了人类文明进步的道路。连续统假设背后就站着人们望而生畏面目狰狞让所有人谈虎变色闻风丧胆的无穷大。一个无穷大都可以把所有数学天才吓得灵魂出窍，两个甚至多个无穷大搅在一起足以让所有人魂飞魄散。

离经叛道神秘莫测的连续统假设在什么样的框架下可以解决？人们依旧一脸迷茫, 一筹莫展, 倍感沮丧。基础数学的停滞不前给现代文明的进一步发展带来难以估量的损失。

数学天才们绝望无助，甚至许多人认定，连续统假设就是一个伪命题，毫无价值，毫无意义。难道高瞻远瞩的希尔伯特错了吗？

一路经历狂风暴雨惊涛骇浪的历史巨轮终于来到了公元2019年。

三、发现

傲视群雄不可一世碾压人类智商100多年的世界头号难题连续统假设终于迎来了它的终极审判日。

通往人类智商的珠穆朗玛峰的悬崖绝壁上终于被劈开一条绝处逢生的险路。

公元2019年三月, 美国硅谷一个车库里, 分数的奥秘被发现了；四月, 分数数域的生成规律和通项公式被发现了；七月, 在中国廊坊, 分数数域的生成率大常数Q和众多反例被发现了；八月, 连续统假设被彻底推翻了。在铁板钉钉的海量数据证据面前, 在严格数学推导的泰山压顶毁灭性的无情铁拳重击下, 连续统假设顷刻间土崩瓦解, 灰飞烟灭。大常数Q彻底砸断了连续统假设的脊梁骨，也彻底砸断了康托尔无穷大理论的脊梁骨。大常数Q打开了基础数学通向无穷大的大门。现在无穷大天门洞开, 千军万马将浩浩荡荡冲将进来。

有人或许会问, 我们小学就玩得滚瓜烂熟的简单分数还有什么神秘的奥秘吗？确是如此。人类第一次发现: 最最简单的分数里隐藏着我们前所未见的极其深刻的宇宙奥秘。这些宇宙奥秘和无穷大息息相关。这些奥秘就是破解世界头号难题“连续统假设”的关键。《大数域原理》一书仔仔细细认认真真回答了如何发现这些奥秘的整个过程。大自然最深刻的规律, 宇宙最深邃的奥秘, 就常常隐藏在我们最司空见惯最习以为常又熟视无睹的地方。这些规律和奥秘常常披着最朴实无华的外衣。发现这些奥秘不难，只是需要超乎寻常的强烈好奇心和耐心。

千百年来, 人们过度迷恋质数, 远远低估了分数蕴涵的无与伦比的巨大力量和极其深奥的自然规律, 远远低估了分数对探索无穷大的极端重要作用, 远远低估了分数生成后面的深刻哲理, 远远低估了分数和所有其他无穷大大数域密不可分的逻辑关系, 付出了沉重的代价。

回顾整个探索发现过程,探索无穷大的本质是对数的探索。数的探索本质上是对分数的探索和对基数的探索。因为分数涉及到一个重大哲学原理, 即中国古代伟大哲学家庄子的无限可分原理；而对基数的探索涉及到另外一个重大哲学原理, 即中国古代伟大哲学家老子的无限生成原理。而探索数学基础框架则是对亚理士多德存在哲学的再思考。这三位人类思想史上的巨人为已经人类整个数学和科学的发展设计了宏伟壮丽的哲学框架, 冥冥之中为人类文明的数学发展指明了方向。

存在属性哲学,无限生成哲学原理和无限可分哲学原理共同构成了数, 数域, 数域基数和数学公理的哲学基础, 也共同构成了基础数学的哲学基础。这三大哲学原理是撬动地球的杠杆的伟大支点(阿基米德语)。没有亚理士多德, 老子和庄子这三位哲学巨人的指引, 数学哲学不可能有任何重大进步, 数学更不可能有任何重大进步。不深刻理解无限生成原理和无限可分原理, 人类不可能征服无穷大和无穷小。不深刻理解亚理士多德的存在属性哲学, 我们不可能彻底理解数学公理的来龙去脉。数的本质让人类困惑了5000多年, 基数尤其是分数集合的基数让人类困惑了100多年。（图2）

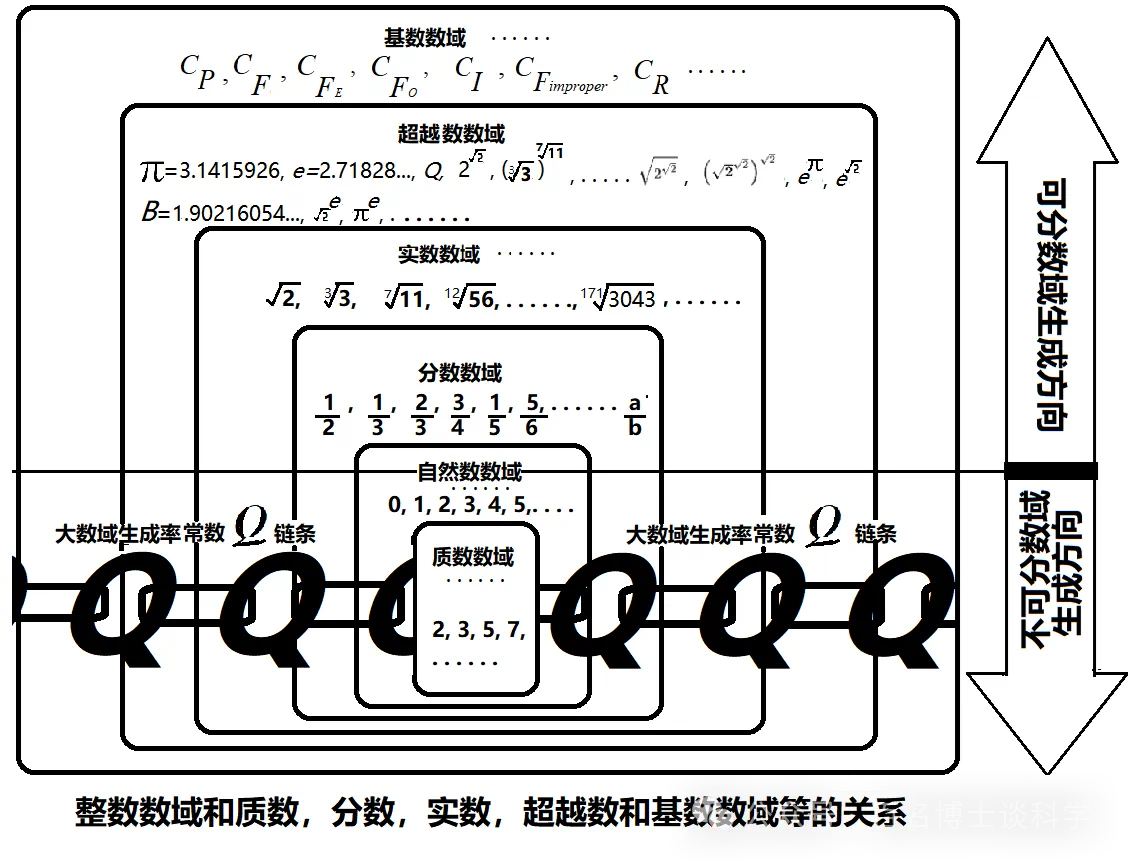
图2

反观康托尔的主要著作，我们发现康托尔的无穷大理论缺乏明确清晰的哲学理论和哲学原理做基础，这是其最大短版。一个伟大的基础理论，一定要阐明自己基础理论的哲学基础是什么，为什么，所依据的哲学原理有哪些，这些哲学原理是怎么指导贯穿自己的整个基础理论，而不是玩弄符号游戏，搞一些花里胡哨昙花一现的东西。

《大数域原理》作者遵循伟大思想家老子的无限生成哲学和和庄子的无限可分哲学原理, 深入研究人类思想史和数学发展史, 深入分析数和基数的来龙去脉, 深入剖析康托无穷大理论的哲学基础, 找出其哲学基础等的致命错误和缺陷, 彻底抛弃康托尔无穷大理论里几乎所有带着许多基因缺陷和致命硬伤的肤浅粗糙混乱不堪的概念和方法如可数集, 阿列夫0, 一一对应映射等, 正本清源, 返璞归真, 回归数学真正的起源和基础－数, 采用正确的客观的不以人们意志为转移的亚理士多德的逻辑思维和亚理士多德, 老子, 庄子的哲学原理为基本世界观方法论和指导思想, 采用强大的现代计算机技术, 作出了一系列有价值的原创发现。在人类历史上首次发现了分数(集合)数域的基数的准确值；发现了分数数域生成率大常数Q；发现了分数数域基数的通项公式以及前所未见的基数数域－一个比所有人类已知的所有无穷大大数域更加宏大的数学基础底盘。（见图2）

在这些发现的基础上, 作者不但揭示了连续统假说在传统数学里无解的根本原因, 指出连续统假设只能在全新的大数域理论框架内才能彻底解决, 还解决了一系列困难度远远超过连续统假设的数学难题, 创建了以大常数Q为基础的大一统数学, 统一整合了所有数和所有无穷大大数域, 更进一步发现了数学公理生成规律, 打通了哲学和数学密切相联的神秘通道, 创建了完全独立于欧几里得等量公理和皮亚诺公理体系的全新的更强大的大数域公理体系。（见图3）

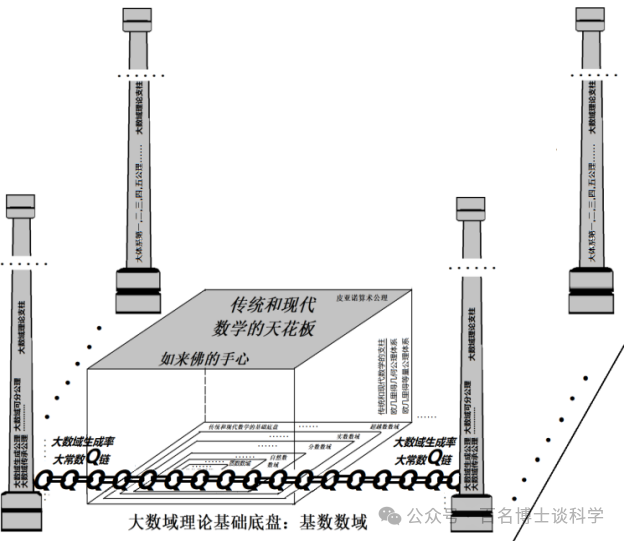
图3

所有的整数都是从0和1生成出来的, 所有数都是从整数生成出来的, 整数数域是从整数生成出来的, 所有无穷大大数域和大数域基数都是从整数数域生成出来的, 完全符合老子的生成哲学原理。

第1：整数数域的基数决定质数数域和斐波那契数域等无限不可分无穷大大数域基数,

第2：整数数域的基数也决定分数数域等无限可分无穷大大数域的基数；

第3：整数数域的基数和分数数域基数决定实数数域基数；

第4：整数数域, 分数数域和实数数域的基数决定超越数数域等无限可分无穷大大数域的基数。

这就是大数域理论发现的无穷大大数域基数生成链。这个基数生成链是经过积年累月海量计算机数据验证的。无穷大大数域基数生成链是大数域理论运用老子无限可生伟大哲学思想和庄子无限可分哲学原理作出的重要原创发现。这些无穷大大数域之间存在自然的深刻的内在的牢不可破的稳定的数值逻辑生成关系, 而不存在人们一厢情愿主观人为设定的表面的肤浅的一一对应映射关系。

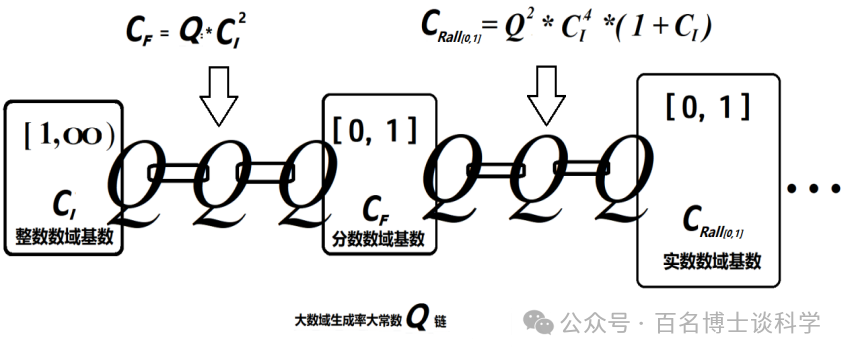
图4

康托尔的传统无穷大理论里的一一对应映射方法在无穷大大数域元素层面完全失效, 无穷大集合的元素在元素层面是无法用建立一一对应映射关系的来判断两个无穷大集合的基数是否相等的。不但连续统假设是错误的, 而且康托尔无穷大理论里的几乎所有有关无穷大基数的结论和计算结果都是错误的。（见图3 和图4）

大数域理论指出：以欧几里得、欧拉、笛卡儿、高斯、黎曼等杰出数学家为代表的传统数学主要研究对象是数和数的关系(数和形的关系, 形和形的关系最后也归结于数和数的关系, 因为数有定位属性可以定位几乎任何几何形状, 数可以定形), 以康托尔的传统无穷大理论虽然研究数和数的关系, 也触及了数和数域, 数域和数域基数关系的天花板, 但至今没有突破这个天花板。见图5。

大数域理论是人类历史上除了研究数和数的关系, 第一次全面探讨数和数域; 探讨数域和数域; 探讨数域基数和数域基数; 探讨数, 数域, 数域基数和数学公理之间错综复杂的关系的数学, 大数域理论完全突破发散无穷大这个几千年来死死压在在人类头顶上沉重的天花板, 看到了发散无穷大这个莫比乌斯带的全貌, 让人类第一次看到天花板上面和莫比乌斯带外面的浩瀚无垠的茫茫宇宙。

大数域理论指出：无限无界无穷大的困难程度和复杂程度远远超出以欧几里得等量公理体系基本理论框架为基础的传统经典数学, 远远超过康托尔的经典无穷大理论的认识深度, 远远超出皮亚诺公理, 罗素公理和策梅洛公理等近代以来所有公理体系的思维范畴, 也远远超过人类已有的所有认知。

大数域理论指出：尽管连续统假设是现代数学的天花板, 是现代数学不可逾越的巨大障碍, 但连续统假设仅仅是大数域理论的地板, 是大数域理论入门级别的练习题, 大数域理论里讨论的几乎所有难题难度都远远超过连续统假设。

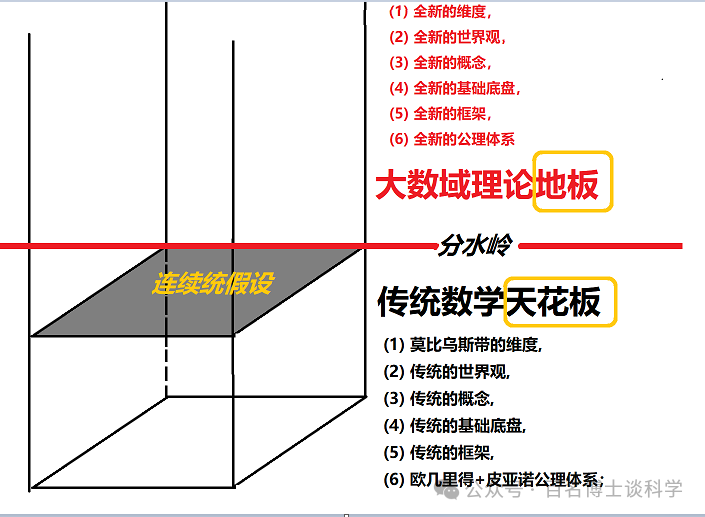
图5

四、验证

怎么验证连续统假设呢？既然发现了大常数Q, 能否检验一下这个Q有什么价值呢？能否用这个大常数Q验证一下连续统假设到底是对是错呢？就是说有没有一个独立公平公正客观的办法, 一个人人可用的试金石来检验一下到底是大数域理论的结论正确,还是康托尔的无穷大理论的正确呢？

有。

验证方法和试金石就是区间[0, 1]里所有分数之和我们可以计算1到10, 1到100,……, 1到100万的所有整数生成的真分数之和, 看看逐步扩展的整数区间所生成的所有分数的计算值和实际值之差是不是收敛, 用最基本的数学知识, 就可以立刻判定孰是孰非，而不需要故弄玄虚故作高深装神弄鬼的复杂冗长的符号游戏把人弄得稀里糊涂晕头转向。

区间[0, 1] 内所有分数之和其难度远远超过连续统假设。根据《大数域原理》一书介绍, 假如连续统假设是正确的, 知道了分数集合的总的个数, 即使康托尔没有发现新的数学公理, 借用大数域原理发现的全新的动态瞬时等差公理, 康托尔应该可以计算所有分数之和这个简单问题, 事实证明, 连续统假设完全乱套了, 根本找不到北, 和真实结论南辕北辙。《大数域原理》计算了连续统假设成立的各种情况的计算结果, 计算值和实际值的误差急剧发散, 全部错误。就是说假如连续统假设成立, 我们仍然无法推导出任何有学术价值有意义的重大数学结论。基础数学仍然无法凭借连续统假设是正确的这一前提取得任何有意义的重大进步。而大数域理论的计算结果是随着整数增加, 逐步扩展的整数区间内所有整数所生成的所有分数的计算值和实际值之差急剧收敛, 而当整数趋于无穷大时误差收敛趋于0, 再一次用铁板钉钉的证据证明了大常数Q和大数域理论的正确。

应该说, 区间[0, 1]里所有分数之和的超级难题不但是大数域理论和常数Q的试金石, 不但是康托尔无穷大理论和连续统假设的试金石, 也是传统数学理论的试金石, 是传统数学能力的极限的试金石。可以说, 传统数学没有任何一个数学学科, 任何一个数学理论, 任何一个数学常数, 任何一个数学方法可以破解这个大数域理论里最简单的所有分数之和的数学题。

连续统假设已经困扰人类超过一个世纪, 而这个区间[0, 1]里所有分数之和的超级难题, 从欧拉算起, 少说也有300多年, 因为欧拉等数学家解决了所有整数的倒数之和就是调和级数求和问题, 而调和级数求和仅仅是所有分数之和的微不足道的一个特例:。

以欧拉的天才敏锐和和经验老道, 自然会举一反三想到比调和级数求和更加一般的所有分数之和的问题, 但是历史记录没有答案。应该不止欧拉, 全世界所有学过中学数学学过调和级数的学生都应该想到, 所有分数之和等于多少。事实上, 不但欧拉无法解出看似简单的所有分数之和的超级难题, 就是高斯, 黎曼甚至康托尔以及百年来的所有天才也不可能解决这个数学难题。因为这是一个属于人类未来数学的难题, 所有传统数学技巧全部失效。如同对于毕达格拉斯来说, 微积分就是未来数学, 让毕达格拉斯计算圆面积函数的导数, 显然勉为其难。沉迷于传统数学的数学家是不可能发现未来数学的伟大规律的。只有挑战和质疑传统数学的勇士才有可能发现和捕捉未来数学的蛛丝马迹。

这里大数域理论再一次展示了其粉碎性碾压传统数学, 毁灭性碾压康托尔无穷大理论的骇人听闻无比强悍的恐怖实力, 展示了大常数Q和大数域公理体系的无与伦比的威力, 小试牛刀, 仅仅在几分钟内, 就可以破解这个传统数学和康托尔无穷大理论永远无法破解的而且难度远超连续统假设的数学难题即区间[0, 1]里所有分数之和的超级难题。

所有分数之和的重大意义在于, 人类第一次找到了分数数域的GDP, 即无穷大分数数域的总量。

分数之和这个试金石有什么意义呢？试出哪些有学术价值的东西呢？分数之和这个试金石检验了:

第一：大数域理论的哲学基础老子的生成哲学和庄子的无限可分哲学是正确的。

第二：大常数Q是正确的；

第三：分数数域基数公式是正确的；

第四：大数域理论发现的动态瞬时等差公理是正确的。

第五：人类可以精确计算任意区间, 任意数轴, 任意平面, 任意曲面, 任意空间里任意类型数(整数/分数/实数/超越数/甚至基数等)的总量。人们第一次掌握了各种类型数的总量的威力, 各种类型数域的总量的威力, 一, 二, 三维空间图形和物体上分布的各类数和数域的总量的威力。这是人类文明和数学史上开天辟地前无古人的壮举。

前四个东西一定要全部正确, 才能确保分数之和计算正确, 缺一不可, 其中第一条哲学基础正确最重要。而这四个重要结论对未来数学都有不可估量的巨大影响和推动作用。站在这四块巨石之上, 我们可以发现更多更有价值的东西。我们可以计算任意区间, 数轴, 平面, 空间, 甚至曲面上所有分数之和, 实数之和, 超越数之和等等, 这些前无古人的重要结论都是千百年来人类梦寐以求的。

需要强调的是，用分数之和验证连续统假设只是大数域理论里众多方法之一，《大数域原理》一书里开列了许多不同的方法证明连续统假设是错误的。这里就不一一列举。

那么康托尔的连续统假设缺了什么东西呢？可以说, 缺的东西太多, 康托尔的无穷大理论甚至不知道分数是从哪里来的, 只知道盲人瞎马随心所欲拉郎配一一对应映射就是了。所以, 即使康托尔的连续统假设是正确的也此路不通, 根本走不下去, 推导不出任何有重大学术价值和意义的重要结论。独臂难支大厦, 连续统假设的错误只是康托尔无穷大理论众多根本的致命错误之一, 其他错误在《大数域原理》里也都一一列举出来。这些错误导致传统无穷大理论问世以来没有取得任何重大进步。

康托尔的连续统假设出现错误不是偶然的, 而是康托尔的整个无穷大理论的框架, 哲学基础, 逻辑基础, 整个世界观和方法论都有严重错误；不是数学技巧和数学推导的问题, 而是大是大非方向性错误导致康托尔理论悖论迭起自相矛盾漏洞百出。对此《大数域原理》一书进行了详细分析。

现代科学迟滞不前的主要原因就是基础数学理论出现重大基础性方向性错误。

五、数学四要素

大数域理论指出：数学的基础是数而不是集合。人类的无穷大探索是数的探索而不是集合的探索。这是大是大非大方向。大方向不对, 后面所有推理结果都是错的。无穷大探索和集合没有一毛钱关系。探索无穷大, 基因缺陷众多的集合概念远远没有数和数域的概念来的深刻, 差光年都不止。

数是本, 函数是末；数是源, 函数是流；数是干, 函数是枝；不变的是数, 变的是函数。函数始于数, 归于数。函数千姿百态, 千变万化, 万变不离其宗, 函数万变不离无穷大大数域, 函数运算结果全部落回无穷大大数域。

大数域理论指出：无穷大大数域是数的大本营, 哪个数域大本营的基数越大, 那个数域的维度就越高, 那个数域的空间就越大, 包含和兼容能力就越强, 所揭示的规律就越深刻, 能够解释的自然现象就越多, 该数域所涉及的规律也就越难以发现, 对未来无穷大大数域的发展影响也越大。而质数数域的基数非常小, 质数数域的规律非常有限, 在无穷大范围, 质数数域对无穷大大数域全局的影响非常非常小, 小到微乎其微, 远不如分数数域对无穷大大数域压倒性的绝对主导的影响来得大。

大数域理论指出, 比传统数学相对简单的数和数的关系更加复杂更加抽象更加深刻的是前所未有的数和基数, 基数和基数, 数和数域, 基数和数域以及数域和数域等错综复杂的关系。

基础数学的发散无穷大四大基本要素是：数, 数域, 数域基数和公理体系。即：

(1) 数：如整数、分数、实数, 超越数等。

(2) 数域：所有无穷大大数域都是由数组成的如整数域、分数域、实数域等。

(3) 数域基数：所有无穷大大数域的基数, 例如整数数域、分数数域、实数数域的基数等。

(4) 公理系统：所有无穷大大数域及其元素适用的公理等。

数,数域和数域基数是数学的基础底盘。公理体系是基础数学理论的支柱和框架。

现在数学的基础底盘彻底变了,数学的支柱和公理体系彻底变了, 数学一定会发生翻天覆地的巨变。随之而来的是所有以数学为基础的基础科学会发生巨变, 世界会发生巨变, 文明会发生巨变。

大数域理论指出：在数学的四大基本要素：数, 数域, 数域基数和公理体系里, 传统数学仅仅研究数和数的关系, 黎曼几何和罗巴切夫斯基的非欧几何也仅仅是扩展欧几里得几何公理的第五公设到更加一般的各种曲面情况, 并没有完全摆脱和超越欧几里得几何公理和算术公理的基本框架, 仍然属于传统数学范畴。就是说自康托尔发现无穷大基数和皮亚诺发现创立算术公理以来, 人类并没有在完全突破欧几里得公理体系和皮亚诺公理体系方面作出任何开天辟地的重大的开创性突破。仍然在传统数学的天花板下面变着花样翻腾各式各样的花里胡哨哗众取宠的跟头把戏。

大数域理论除了研究前三个要素的所有六种不同组合：数和数,基数和基数, 数和基数, 数和数域, 基数和数域, 数域和数域的关系以外, 还特别构造与欧几里得算术公理的基本框架完全不同的大数域公理体系, 以解决全新领域开辟后遇到的前所未见的新的数学难题, 而这些难题是传统数学和传统公理体系完全无能为力的。大数域理论在人类历史上第一次解决了数和基数, 基数和基数, 数和数域, 基数和数域以及数域和数域的关系之间基本关系的重大基础理论问题, 解决了如何建立完全不同于欧几里得算术公理的基本框架的全新公理体系框架的问题, 还进一步解决了数学公理的基础和来源的问题。

如果我们不积极寻找数学公理生成的一般规律,我们只能世世代代局限在欧几里得公理体系而无法发现更加伟大的数学框架, 无法发现更加宏伟深刻的宇宙最底层规律, 无法探索更神秘更深奥的宇宙奥秘, 将永远满足于徘徊在一些看似高深莫测其实都是技巧性重复性娱乐性的低端的初级的数学题目上, 年复一年的做着鸡毛蒜皮边边角角零零碎碎可有可无毫无价值哗众取宠的东西, 满足于自吹自擂自欺欺人自娱自乐自我陶醉自说自话却以为是有意义的事情上, 白白浪费宝贵资源而无法突破我们固有的根深蒂固的传统认知边界去破解宇宙真正的奥秘, 去提升我们的当前文明到一个更高级的阶段。

大数域理论除了深入讨论形形色色各种类型的数到底是什么,数的来龙去脉以外, 还探讨了一个几乎无人关注的但却是更加重要的数学哲学问题, 就是数学公理的来源和来龙去脉。

数学公理的基础到底是什么？数学公理的起源到底是什么？是什么因素决定数学公理的存在？

这是比连续统假设深刻得多, 重要得多, 影响深远得多, 意义也重大得多的数学哲学基础理论问题。

《大数域原理》初步探讨了这个极为沉重严肃的话题。试图揭开数学公理的奥秘,探索数学公理的来龙去脉, 找到数学公理生成的一般规律, 找到人类文明数学各类数学学科比如代数, 三角, 几何, 微积分, 微分几何等等学科的一般生成规律, 仔细考察这些数学学科的基础底盘是什么, 公理框架是什么, 当前基础底盘外面还有什么, 当前公理框架外面还有什么, 最重要的是它们的哲学基础是什么以及正确与否, 这些数学学科的存在是否具备正当性, 客观性和合理性而非人们主观凭空捏造胡编乱造毫无价值哗众取宠昙花一现的漂亮的肥皂泡沫。《大数域原理》还讨论了到底有多少数学基础底盘? 未来到底还有多少数学常数没有发现? 为什么人类几千年来一直没有发现比更伟大更重要的常数？未来到底还有多少数学公理没有发现? 未来到底还有多少数学学科没有发现? 人类在数学上到底能走多远？人类在文明进化阶梯上到底能走多远？为什么？根据是什么？回答和解决这些问题是大数域理论和传统数学的根本区别。也是康托尔经典无穷大理论望尘莫及的。见图6。

大数域理论深入探讨了古希腊人类的伟大先哲亚理士多德的存在哲学,对亚理士多德提出的存在哲学理论的存在属性(第一属性)和第二属性进行深入思考, 提出了存在的存在属性即第一属性是基本属性而第二属性是特征属性。按照亚理士多德思想, 存在的所有的第二属性特征属性都是存在的第一属性的从属属性。大数域理论首次提出

(1)每个存在都有一个第一属性即存在属性和无穷多个第二属性即从属属性或特征属性；

(2)宇宙有无穷多的存在；

(3)所有无穷多的存在的第一属性和第二属性都是显性属性；

(4)每个存在还有无穷多的隐性属性；

(5)存在的无穷多隐性属性会在其发展的不同时期和阶段会转变为存在的无穷多的显性属性；

(6)无穷多的存在的无穷多的显性属性的各种组合会生成无穷多的数学公理；

(7)这些无穷多的存在的无穷多显性属性和无穷多的数学公理可以组合成无穷多的数学学科；

(8)人类发现的屈指可数的几个数学公理和数学学科与浩瀚宇宙相比微不足道；

(9)和宇宙无穷无尽奥秘相比,迄今为止人类数学的所有成就只是烧了几块有许多瑕疵裂缝的砖瓦而已, 而不是法国数学家庞加莱说的已经建好的数学大厦, 准确说连鸡窝都算不上。

(10)数学连地基都没有建好,集合不是数学的基础。数学的未来还有无穷无尽的发展可能性。

如果数和无穷大大数域出了问题,那一定是惊天动地天塌地陷的大问题。没有数, 就没有函数, 就没有数学, 现代文明寸步难行。因为现代文明赖以生存的基础是数学, 而现在数学的基础底盘大数域出了大事。

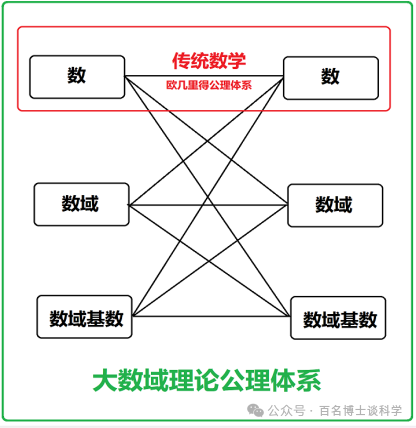
图6

大数域理论指出, 第一, 在整数数域和分数数域之间, 存在无穷多个无穷大大数域其基数大于整数数域基数而小于分数数域基数；第二, 在分数数域和实数数域之间, 存在无穷多个无穷大大数域其基数大于分数数域基数而小于实数数数域基数。大数域理论给出了严密清晰的哲学原理解释, 完整的数学推导和海量计算机数据的证据, 彻底推翻康托尔的连续统假设。

大数域理论指出：不但整数, 偶数, 奇数和质数的无穷大大数域的基数不同, 而且整数, 偶数, 奇数和质数生成的不重复分数数域的基数也是不一样的；不但整数, 偶数, 奇数和质数的无穷大大数域的基数互相关联, 而且整数, 偶数, 奇数和质数生成的不重复分数数域的基数也是互相关联的。和整数, 偶数, 奇数生成的不重复分数数域的基数相比, 质数生成的不重复分数数域的基数最小而且是无穷小, 是一条微乎其微的细线，可以忽略不计。几千年来人们趋之若鹜津津乐道的质数在无穷大大数域的生成和发展过程中的贡献为无穷小, 对未来无穷大大数域的发展没有任何重大影响。见图7。

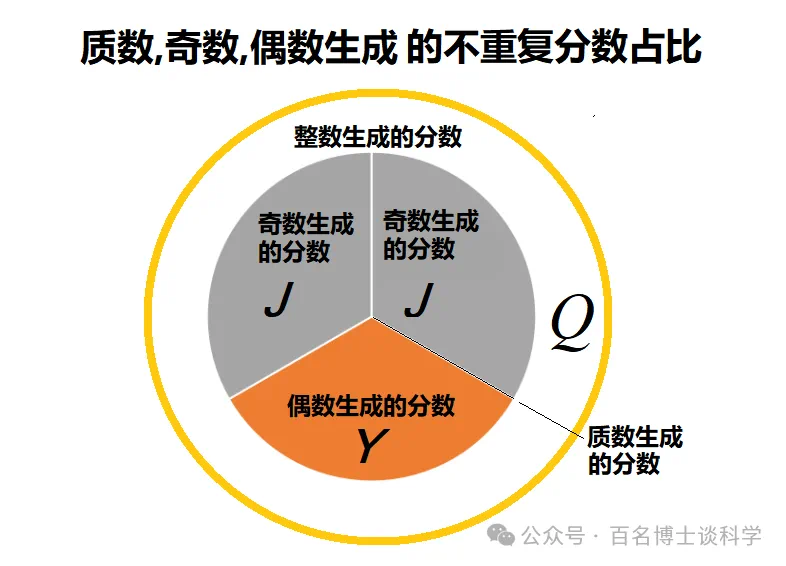
图7

由图7可看出, 组成整数的偶数和奇数生成的分数个数是一定的, 而且奇数生成的分数个数是偶数生成的分数个数的2倍。《大数域原理》一书已经给出完整的纯数学推导证明和计算机数据证据。从图7我们可以得到什么启示呢？图7和《大数域原理》的数学推导告诉我们, 整个分数数域的个数或基数可以干干净净的分成三等分, 其中一份是全体偶数生成的, 其它两份是全体奇数生成的；由于整个质数数域包含在奇数数域里面, 所以不需要另外单独计算整个质数数域元素生成的分数个数。这个分析给我们启示如下, 大常数Q一定可以被3整除。而大常数Q的每个个位里可以被3整除的数只有0, 3, 6和9, 所以大常数Q一定全部是由0, 3, 6和9组成。

由图7还可看出,由于质数数域生成的分数数域, 实数数域以及超越数数域的基数都远远小于整数数域, 偶数数域和奇数数域生成的分数数域, 实数数域以及超越数数域的基数, 是无穷小。质数域对无穷大大数域的整个生成发展已经无足轻重。在无穷大大数域的基础数学领域, 除了一些实际应用, 质数基本成了昨日黄花, 失去了昔日春光无限英气逼人的风采, 失去了言必称质数的往日辉煌, 质数将慢慢淡出无穷大的历史舞台；只有分数尤其是基数风头正劲, 摧坚挫锐, 披荆斩棘, 气吞山河, 势不可当, 挟电携雷, 叱咤风云, 一展雄风, 浓墨重彩书写波澜壮阔的人类文明史上最新最美的画卷。

六、大一统数学

把所有分门别类的数学学科统一起来, 建立大一统数学, 是古往今来几乎所有数学家梦寐以求的目标。统一什么？在什么数学基础和哲学基础上统一？用什么基础理论和数学工具统一？统一后会有什么翻天覆地的效果？这是大一统数学要解决的问题。

大数域理论指出：大一统数学最核心的哲学基础是存在属性哲学, 无限生成哲学和无限可分哲学；大一统数学最核心的是基础数学的统一；基础数学的统一关键是数学基础底盘即各类数的统一；数学基础底盘的统一关键是形形色色无穷大大数域的统一。

大数域理论指出：迄今为止几千年来, 人类今天所有辉煌文明成果都一直是建立在离散的, 互相隔离, 互不联通, 一盘散沙, 支离破碎的无穷多个无穷大大数域基础上的, 即质数数域, 整数数域, 分数数域, 实数数域, 超越数数域乃至基数数域, 都是各自为政, 互不相干, 互不联通, 完全独立, 支离破碎的, 没有形成一个统一的完整的有机的整合的整体。大数域理论第一次把这些毫不相干的无穷大大数域整合在一起, 找到了它们之间内在的数值逻辑关系。大数域理论创立之前, 人类文明没有发现这些无穷大大数域之间存在任何内在的密切相关的不以人们意志为转移的客观规律。

大数域理论指出：未来的数学一定是无穷大的世界。未来文明可能是Q的文明。

今天，大数域理论把这些亘古未见的大一统数学的伟大规律揭示出来。

数是数学的基础,数学是科学的基础, 科学是技术的基础, 科学技术是文明的基础。

一个残缺不全一盘散沙的传统基础数学底盘都可以创造如此辉煌灿烂的现代文明,那么一个完整的整合的互相联通的大一统的无穷大大数域会给人类文明进步带来怎样翻天覆地的变化, 已经远远超出我们有限的想象力。见图8。

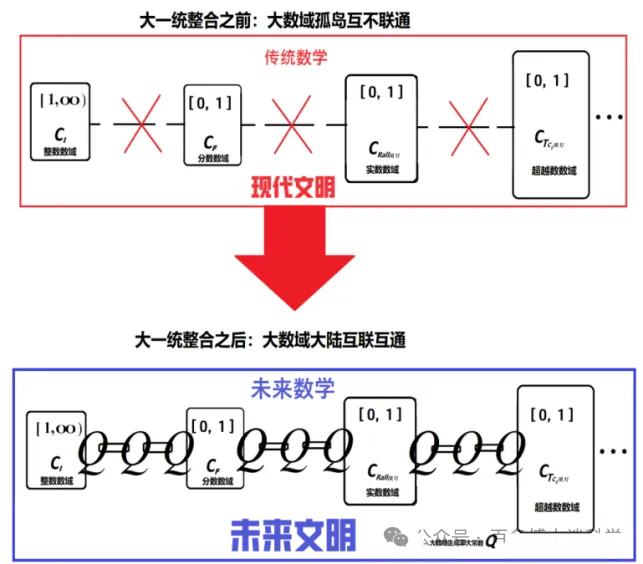
图8

可以预见的是, 一个整合的互相联通的大一统的无穷大大数域和大一统数学将创造一个前无古人的更加光辉灿烂的未来文明。

没有传统数学就没有人类现代文明；同样没有无穷大大数域就没有人类未来文明。

无穷大大常数Q就是人类建造的驶向真理的彼岸, 驶向茫茫宇宙深处, 驶向未来高阶文明乘坐的未来数学巨轮的龙骨。

我们盼望大数域理论能够为开启人类文明升级为星际文明的新纪元贡献绵薄之力。

七、小结

发现偏爱好奇的心，真理垂青勇敢的人。

爱因斯坦说：我并非天赋异禀，我只是有强烈的好奇心（“I have no special talents, I am only passionately curious.”）。

伟大的好奇心产生伟大的发现。

最后总结一下大数域理论的一些主要发现：

第一：首次发现无限无界无穷大分数数域与整数数域元素之间不存在表面的肤浅的人为主观的, 极其牵强附会的表面的片面的静态的生硬僵化的所谓一一对应的映射关系；而存在客观的严密的深刻的稳定的内在的动态的不以人们意志为转移的数值运算逻辑生成关系；即所有分数都可以由所有整数生成, 整个分数数域可以完全由整数数域通过同样的数值运算生成。因此, 分数数域的基数完全由整数数域的基数决定, 而非由一一对应的映射关系决定。

第二：首次发现大数域分数生成定理：分数数域的基数和整数数域的基数的平方成正比, 首次发现分数数域的基数的数学通项估值公式。整数数域基数决定分数数域基数。

第三：首次发现联接整数数域和分数数域之间的关键常数大数域分数生成率Q。该分数生成率大常数Q可以和人类所有文明和不同民族共同发现的人们熟知的伟大常数的圆周率常数相媲美；但是发现维度更高, 难度更大, 领域更广泛, 发现过程更加艰苦。由于大常数Q涉及无穷大大数域, 而只是几何里一个特定图形圆的直径和周长关系, 不涉及无穷大, 我们猜测：Q在未来数学的重要性将远超常数。

第四：首次发现人们熟知的实数数域和超越数数域之外还存在一个人类完全未知的更加宏大的基数数域或超(级)数域, 该基数数域或超数域和所有已知的传统的常规数学数域如整数数域, 分数数域和实数数域, 超越数数域等等都完全兼容, 所有已知的传统的常规数域只是基数数域的其中某一个局部数域(或子数域), 且各个数域之间既互相独立又息息相关, 密不可分。

第五：首次严格区分元素存在的各种不同属性, 特别强调元素存在属性的第一优先的极端重要性以及在无穷大复杂情况下以元素的从属属性对元素分类方法的局限性和存在的基因缺陷。大数域理论认为, 数的本质是对存在的描述的更为抽象的存在, 即数是存在的存在, 是超级或特殊的存在, 或者说数本身就是存在。人们认识或认知的数是由依附于数的存在属性的数值属性和定位属性所体现的特殊度量功能来表达数域元素及其各种相同或不同属性之间的相互联系。

第六：首次发现整数和分数数域里都包含无穷多对客观存在的不同基数值的孪生数域。

第七：首次发现基数具有极其诡异的常量变量二象属性, 最令人吃惊的是基数作为无穷大的一个度量单位具有如此神秘的诡异性质, 在不同维度不同参照系具有完全不同的特性, 无穷大基数的常量变量二象性是造成人们难以理解无穷大实质的关键。

第八：首次发现无穷大基数反比定理, 即无穷大数域基数和数域元素的相对或绝对发散速度成反比, 为判别比较无穷大数域基数之间的大小找到快速判别法。

第九：首次发现极为抽象的不为人知的数域生成维度, 将人们认识数的思考和观察维度从传统的元素个案维度提升到数域生成维度的体系思维, 以动态的全新的开放的观点从数域生成维度来认识客观世界和解决客观事物本质问题, 实现了人们对数的认识从之前基于元素个案的初级的感性的静态的碎片的局部的肤浅认知上升到基于体系的由维度构成的动态的发展的整体的深刻认识的质的转变和根本突破。

第十：首次运用基数数域概念, 数域生成维度概念和大数域理论, 为解决经典的集合论里原本存在多年的一直争论不休的一系列诸多经典疑难问题提供了全新的大数域整体高维度解决方案。

第十一：大数域理论展示了极其强大的整合传统数学所有辉煌成果的卓越的能力。在动态大视角高维度思维引导下, 大数域理论成功地用独立发现的分数数域生成率大常数Q把原本离散的毫不相干的完全独立的质数数域、整数数域、分数数域、实数数域和基数数域等几大数域创造性地整合成为一个紧密相连, 息息相关的一个大数域整体, 使得所有传统的数值运算法则和公式常数等在所有数域里全部通行无阻, 并行不悖。大数域理论不但能够整合所有传统数域, 还能够整合传统数学, 可以传统数学为基础, 从低维度数域的个别公式的简单个案提升, 到更高维度和抽象归纳, 再到更加一般和普遍的现象, 在更大规模的基数数域领域里发现和揭示出比原先个别公式更加深刻更加广泛更加具有一般意义的客观规律。大数域理论的强大兼容性和整合性是一种更加广义更具有一般意义的有效性、自洽性和完备性的进一步拓展。大数域理论和原有的传统数学是完全整合的和一脉相承的。和传统数学理论相比, 大数域理论的数域底盘更大, 公理体系支柱更多, 维度框架更高。

第十二：大数域理论几近无限地拓展了传统极限理论里经典的洛必达法则处理的一些极端情况的难题。并用自身独有的赋能优势全部赋予其完整的全新的意义, 在更高的数域生成维度推出了完整的体系性整体解决方案。使得原先在低维度处理极端情况的传统极限理论的洛比达法则成为高维度大视野的大数域理论的一个低维度特例。

第十三：首次在无穷大探索领域突出强调保持逻辑推理的前提的正确性和一致性公理是确保获得逻辑推理正确结论的极端重要的首要前提, 是无穷大逻辑推理的第一优先；首次强调突出无穷大探索的前提的正确性和一致性的极端重要性, 是揭示客观真相的重要组成部分；首次强调提升维度的极端重要性, 强调高维度思维是揭示客观真相, 发现客观规律的关键因素和第一优先。

第十四：首次系统提出无穷大新框架的高维度思维和逻辑推理必须遵循的五个基本公理：维度公理, 规范公理, 证据公理, 兼容性公理和一致性公理。即任何全新的数学理论, 必须具备高维度优势, 必须遵守维度公理, 规范公理, 兼容性公理, 一致性公理和证据公理；必须和传统数学理论相兼容。兼容性就是容许差异, 接纳差异, 承认特例, 包容事物间有差异的存在。传统数学理论更多情况下只是更高维度大数域理论体系里的一个个特例和个案。大数域理论可以解释传统数学理论的所有现象, 反之则不成立。大数域理论承前启后兼容包含传统经典数学, 集传统经典数学的所有辉煌成果之大成, 同时依据分数生成率大常数Q的独立发现, 完全独立和自成体系地开辟出源于传统经典数学、但是视角的广度、立场的高度和思维的深度等都远远高于和深刻于传统经典数学的脱胎换骨的原创性的全新的大数域领域。

第十五：首次创立了基于大数域分数生成率大常数Q.构建的大数域基础理论框架和基础理论体系, 发现各个无穷大数域之间是以不同的基数为纽带紧密联系在一起的。在该基础理论框架内清晰地界定和规范了一系列便于人们探索无穷大所必需的大数域运算规则和基础理论框架体系, 成功地将高维度里数域生成维度的基数数值的运算与低维度里传统经典数学常规数域中普通数的运算完美统一起来, 有机地继承, 有效地兼容和完整地整合了传统经典数学, 使得后来的人们可以站在我们的肩上, 继续进行无穷大未知领域的探索和发现。

第十六: 首次提出大数域生成公理, 始于原点0的步长为最小整数元素1生成整数数域；整数数域生成其他数域如质数数域, 分数数域, 实数数域, 超越数数域以及基数数域等所有数域；整数数域元素间加减乘除幂运算的基本数值运算就是这些数域的基本生成规则。在整个人类文明发展过程中, 中国古代伟大哲学家老子的生成哲学和庄子的无限可分哲学对数学发展展示出无与伦比的威力。

第十七：首次发现数学公理的生成机理, 发现数的存在决定存在的相关属性, 存在相关属性生成相应公理体系, 公理体系生成相应数学学科的完整的生成逻辑过程。公理与存在息息相关。数的存在属性决定数学公理。数学公理的基础是数的存在属性。

第十八：首次发现数学和哲学的完整生成逻辑链：根据大数域理论, 宇宙中有无穷多的存在, 存在有无穷多的隐性属性, 在存在的无穷无尽的生成演化过程中, 存在的无穷多的隐性属性可以在不同生成演化阶段转化成形形色色无穷多的显性属性, 这些穷多的存在的无显性属性可以生成出无穷多的数值逻辑关系和数学常数, 这些存在的无穷多的显性属性的各种组合可以生成出无穷多的数学公理, 这些无穷多的存在和存在的显性属性加上无穷多的数学公理的各种组合, 可以生成出无穷多的数学学科。迄今为止, 人类仅仅发现60多个包括在内的普通数学常数, 几十个基础和应用数学学科, 大数域理论仅仅发现以大常数Q为代表的十几个大系统无穷大超级数学常数, 但是和无穷大的宇宙奥秘相比完全可以忽略不计。人类文明探索宇宙奥秘的万里长征才刚刚起步。人类仍然是摇篮里的婴儿, 才刚刚睁开迷茫好奇的眼睛。

第十九: 根据公理与存在互相关联和存在决定公理的哲学原则, 大数域理论不但拓展了皮亚诺的算术公理, 更完全独立的创立了一个包含大数域理论生成公理, 大体系公理, 可分公理, 传承公理, 可遍历公理和瞬时等差公理等强大的完整的全新的大数域公理体系。大数域瞬时等差公理是大数域理论运用庄子无限可分伟大哲学思想发现的重要成果。大数域动态瞬时等差公理是说，根据庄子无限可分哲学原理，区间[0，1]里所有分数形成的分数序列，是一个无穷小近似等差序列。

第二十：首次应用发现的大数域生成率大常数Q解决了一系列难度远远超过连续统假设的难题, 并获得计算机海量数据的检验证据, 为否定康托尔的连续统假设提供铁证, 最简单的就是区间[0, 1]里所有分数值之和的通项公式:

第二十一:首次发现在整数数域和分数数域之间, 存在无穷多个无穷大大数域其基数大于整数数域基数而小于分数数域基数；在分数数域和实数数域之间, 存在无穷多个无穷大大数域其基数大于分数数域基数而小于实数数数域基数。大数域理论用铁一般的事实彻底推翻康托尔的连续统假设。

第二十二: 首次提出大数域积分的概念, 使得传统数学里一团乱麻的无穷大积分有了清晰准确的积分数域, 积分范围, 和积分目标。

第二十三:初步揭开让人望而生畏的恐怖的数学黑洞区间[0, 1]的神秘面纱。

第二十四:大数域理论计算了区间[0, 1]的所有分数之和以及实数之和, 计算了整个一维数轴上所有分数之和以及实数之和, 还计算了整个二维平面上所有分数之和以及实数之和, 更计算了整个三维空间里所有分数之和以及实数之和。人类第一次计算出了任意区间, 平面和空间里所有分数, 所有实数甚至所有超越数的综合实力和总量。从此人类掌握了数的综合威力, 掌握了无穷大大数域的综合威力, 掌握了无穷大大数域的GDP。这是数学史上开天辟地划时代的辉煌成就。没有连续统假设的破解, 没有大数域理论的发现, 人类要走到这一步还不知道要猴年马月。按现在康托尔无穷大理论进步的速度, 别说下一个一百年就是一千年也不可能取得这一成就。因为康托尔无穷大理论犯了原则性方向性方法论的重大原则错误, 走上了错误的轨道, 无药可救。要破解无穷大, 只能另起炉灶, 推倒重来。

第二十五:大数域理论提出, 数学研究应该以探索发现为导向；以面向存在的显性属性以及隐性属性的发现, 面向数学常数的发现, 面向存在属性的发现, 面向存在本质的发现为导向；特别是以面向探索自然规律和宇宙终极奥秘为导向；而不是单纯以面向为证明而证明和在故纸堆里找毫无价值的纯粹符号游戏的自娱自乐的所谓难题的数学研究为导向。

第二十六:纠正了伟大数学家欧拉和印度数学天才拉玛努金的关于无穷大的推导错误。他们在完全没有无穷大基数的基本概念情况下，仅凭有限的欧几里得的框架知识，近乎随心所欲随随便便就推导了一些错误结论。例如他们推导的著名的公式就是错误的。

….……

大数域理论彻底破解连续统假设,彻底化解第三次数学危机。

我们的最新研究显示，第二次数学危机仍然存在巨大隐患，并没有彻底化解，人类需要另外一次数学革命。三次数学危机都是由人类无知引起的。

八、贡献

几千年来,中华民族在人类文明最基础最重要的基础数学领域是0贡献, 数学常数是0贡献, 基础数学理论是0贡献, 数学公理是0贡献, 原创数学学科是0贡献, 原创基础数学框架是0贡献。

《数学手册》是集人类最高智慧辉煌成果之大成, 是人类文明伟大结晶的传世杰作, 是人类文明进步最伟大的标志，可惜的是这部人类文明的伟大的旷世巨著没有一个公式, 没有一个常数, 没有一个学科, 没有一个原创理论, 没有一个体系和框架是中华民族贡献的。几百年来直至今日, 我们一直在享用着全世界其他优秀民族的原创贡献而没有任何伟大的开拓性原创付出, 倍感汗颜。

伟大的英国工业革命以来,在那一波又一波世界优秀民族你追我赶争先恐后奋不顾身勇往直前冲击人类文明智商珠穆朗玛峰的探险队里，在现代文明奥运会的文明进步接力赛的世界英豪队伍里, 始终没有出现炎黄子孙优秀儿女英姿飒爽伟岸挺拔的身影。因为这个艰苦卓绝的人类智商珠峰冲顶突击队，这个文明接力赛世界英豪队伍的选手入选条件极其苛刻, 下面8条至少过半才有资格入选冲顶接棒：发现一个前无古人的全新的数或数域，比如希帕索斯的无理数和康托尔的基数；发现至少一个伟大的原创公式, 比如欧拉公式；发现至少一个伟大常数比如欧拉常数 e, 发现至少一个伟大定理/定律比如开普勒定律(鸡毛蒜皮定理/定律无效)；发现至少一个原创公理比如欧几里得几何公理和算术等量公理；创立至少一个原创学科比如牛顿力学；创立至少一个原创理论比如爱因斯坦相对论；创立至少一个原创体系和框架比如爱因斯坦时空体系和框架或高斯和罗巴切夫斯基的非欧几何框架。可以检验, 只有欧几里得, 开普勒，笛卡儿, 牛顿, 莱布尼兹, 法拉第, 欧拉, 高斯,爱因斯坦, 康托尔等几个屈指可数开天辟地的伟大英雄选手入选，其中德国英雄占了一半, 英国两个，法国一个，古希腊一个，瑞士一个。这些卓尔不凡的人类英雄所代表的优秀民族都是今天世界强国。正是由于这些彪炳史册的伟大英雄们前赴后继义无反顾的不懈努力, 人类的文明得以生生不息，磅礴向前。

九、难度

前面说了入选人类文明发展顶级推手的几个苛刻前提和条件，选手们必须：

1).发现一个前无古人的全新的数或数域，比如希帕索斯的无理数和康托尔的基数；

2).发现至少一个伟大的原创公式, 比如欧拉公式；

3).发现至少一个伟大常数比如欧拉常数 e, （尽管e是许多数学家共同发现，欧拉计算的）；

4).发现至少一个伟大定理/定律 比如开普勒定律(要用放大镜找的鸡毛蒜皮定理/定律无效)；

5).发现至少一个原创公理比如欧几里得几何公理和算术等量公理；

6).创立至少一个原创学科比如牛顿力学；

7).创立至少一个原创理论比如爱因斯坦相对论；

8).创立至少一个原创体系和框架比如爱因斯坦时空体系和框架或高斯和罗巴切夫斯基的非欧几何框架。

问题来了，这些发现的难度如何呢？可以按照难度系数从大到小排序一下吗？

我们按照这些前提和条件下人类发现的困难程度划分10个等级，从1到10，1最简单，10最困难。从比较困难到最困难；发现的数量以及百年为单位被发现的概率，来排序这些发现的困难程度。

《大数域原理》指出，最困难的是原创体系和框架，这个是世界观层面的，数量也是最少的，在大数域公理体系发现之前只有2个，欧几里得公理体系（包括几何公理和算术等量公理体系），和皮亚诺公理体系，非欧几何仍然属于欧几里得公理体系。难度是10；被发现的概率大约是一千年到两千年。

其次是数学公理，但凡有全新的有价值的公理发现，一定引起惊天动地的数学革命，而无效数学公理不会引发任何变革，比如罗素公理，策梅洛公理，康托尔公理等都毫无价值，属于没有搞清数学公理来源想当然闭门造车的产物。人们无法从这些公理出发，推导出任何有重大意义和重大学术价值的数学结论。因为有重大学术价值的数学公理一定要有明确清晰坚实的哲学基础，要指向存在特定的存在属性；人类文明史上真正具有伟大学术价值的原创数学公理在大数域公理体系发现之前只有两个，欧几里得公理（包括几何公理和算术公理）和皮亚诺公理（生成公理）；数量2也是最少的，难度10；被发现的概率大约是一千年到两千年。

再其次是数或数域以及数域基数，数量也是最少的，大家熟悉的整数，分数，实数，超越数，复数，基数等等加在一起不超过10个，难度也10；被发现的概率大约也是一千年左右。

接下来是伟大常数，因为数学常数的发现非常困难；数量很少的，大约60多个；难度9；被发现的概率大约是300-500年左右。

接着是数学原创学科和原创理论，又分基础理论数学原创和应用数学原创，而基础理论数学原创最难，大约屈指可数，难度9，而应用数学原创数量较多，大约几十个，难度7到8。只要不是研究数，数域，数域基数和公理体系的数学学科都是应用数学范畴而不在基础数学范围之内，被发现的概率大约是300年左右。

紧跟着是伟大数学公式，伟大数学公式是指揭示宇宙最底层逻辑，跨界整合看起来毫不相干的各种数学体系和常数的公式，其发现也非常困难，非常稀缺，普通公式千千万万，但是揭示宇宙底层逻辑的伟大公式极其稀缺大约十几个，数量不到100个；难度6；被发现的概率大约是200年左右。

最后是伟大定理/定律，伟大定理/定律也是指揭示宇宙最底层逻辑，跨界整合看起来毫不相干的各种宏观和微观的自然规律，其发现也很困难，也属于稀缺品种，普通定理/定律也是数不胜数，但是揭示大自然规律的伟大定理/定律理论寥寥无几，大约几十个，难度5；被发现的概率大约也是100 - 200年左右。

所以根据这些比较客观的量化指标，数学发现乃至科学发现的困难程度排序如下：

数学原创体系和框架> 数学公理 > 新的数或数域> 数学常数> 原创学科> 原创理论> 伟大公式 >伟大定理/定律。

十、转机

中华民族,泱泱大国, 广土巨族, 辉煌文明。

这个举世瞩目的现代文明奥林匹克进步接力赛,这支牵动亿万人心的人类智商珠峰冲顶突击队，这场全人类共同的文明升级的波澜壮阔的伟大事业，岂能缺了我们伟大的中华民族。

在这个人类文明面临重大转型升级的关键时刻，炎黄子孙大展身手的机会来了。

这个伟大古老的民族在沉默几千年后终于伸出她气吞山河移星换斗扭转乾坤的巨手，把误入歧途深陷泥潭的文明巨轮引向正确的航道。

今天从《大数域原理》开始,炎黄子孙实现数学基础理论原创0的突破, 《大数域原理》的数学基础理论的体系性贡献一次性补齐所有重大缺失。

公元2019年,大数域理论元年。

今天中华民族可以大大方方堂堂正正邀请全世界所有民族分享自己炎黄子孙的发现。坦坦荡荡充满自信地伸出自己宽厚坚实的肩膀,让全世界所有其他民族可以站在中华民族的肩上, 为人类文明进步作出更加伟大的发现, 把人类文明提升到一个前所未有的阶段。

山外有山，天外有天，人外有人。团灭欧美超级数学军团, 横行霸道一个多世纪的连续统假设这个前无古人的巨无霸栽在炎黄子孙手里并非偶然。沧海桑田，斗转星移。只要开启民智，受到同样良好的现代文明教育，伟大古老华夏民族，不但能够发明推动人类文明重大进步的造纸术、指南针、火药和印刷术，更可以用自己民族的卓越的抽象力和想象力以及超高智商破解宇宙奥秘最底层的逻辑，发现大自然最深奥的规律，为人类贡献前无古人的未来基础数学理论。

当我们历经艰难困苦在追求真理的崎岖道路上跋山涉水的时候，我们发现炎黄子孙对大自然的发自内心的热爱，对真理无比虔诚执着的信仰，对探索宇宙奥秘的超乎寻常的好奇心，克服千难万险的严酷考验的坚韧不拔的毅力，洞穿事物本质的敏锐洞察力和智商，不输世界任何一个优秀民族。

《大数域原理》说明,炎黄子孙不仅仅是从1到100的优秀的模仿者和跟随者, 不但能够在其他优秀民族的伟大天才发现和创立的基础数学和应用数学的宏伟框架里作出出色的拓展性工作成为出类拔萃的耕耘者, 更可以成为从0到1的开天辟地独树一帜拨乱反正的伟大原创的勇敢的创造者和开拓者。千百年后我们的子孙可以扬眉吐气骄傲的说, 在未来人类文明进步的天梯里, 有我们中华民族贡献的一级阶梯。全人类世世代代子子孙孙可以踩着中华民族贡献的这一级阶梯继续攀登。

在中华民族贡献给未来人类文明进步天梯的那一级阶梯上,镌刻着一个光芒四射的大写的Q字。

十一、后记

得道多助。

仅凭一己之力,作者最大力量是计算大常数Q到整数的10^6, 这还是在个人计算机上日夜不停连续计算2个月才获得的结果。因为每增加一个数量级, 计算量和计算时间会增加100倍, 非常恐怖。

为了尽快占领人类智商的制高点,我们寻求中华民族最优秀的民族精英的帮助。

在计算,追踪和确认宇宙神秘大常数Q的激动人心的日子里, 组织能力出类拔萃的北京孙荷丽女士极尽她最大的力量出色的组织了10^7和10^8的计算, 付嘉先生在阿里云上首先计算10^6, 有趣的是由于计算量太大, 程序运行第一天就被阿里云判为恶意程序停止运行, 最后转而寻求刘佳帅先生在计算机上用CUDA编程在GPU上昼夜不停连续运行43天才完成10^8的计算, 确认常数Q的神秘身份并确认Q的前六位全部是3, 6, 9组成。在此特向参加大常数Q计算的孙荷丽女士, 付嘉先生和刘佳帅先生表示作者最崇高的敬意, 这些民族精英在为中华民族抢占人类智商制高点的关键时刻, 挺身而出, 义无反顾, 作出了不可磨灭的卓越贡献。如果用我们自己的计算机, 计算108生成的分数估计要60万天, 大约1643年。

本书作者欢迎全世界数学家科学家和热爱科学热爱真理热爱探索发现的朋友验证, 质疑, 批判甚至推翻我们的发现, 尤其是希望大家验证我们原创发现的大常数Q, 我们已经极尽自己微薄之力, 计算到一个亿100000000整数即10^8生成的超级大常数Q, 也仅仅看到这个伟大的超级常数Q的冰山一角。我们热切盼望全世界精英可以计算到10^10, 10^100, 10^1000, 10^10000, 10^100000, 10^100000000, .....生成的Q, 揭开这个人类历史上前所未见的伟大的超级常数Q的庐山真面目。我们想看看这个伟大的超级常数Q将会给世界, 给人类, 给我们的整个文明带来怎样翻天覆地的变化。因为这是人类历史上第一次原创发现无穷大大系统之间的超级大常数。

据谷歌搜索, 2021年8月17日,美国趣味科学网站报道, 瑞士研究人员使用一台超级计算机, 历时108天, 将著名数学常数圆周率计算到小数点后62.8万亿位, 创下该常数迄今最精确值记录。人类把这么多资源花在计算传统数学常数圆周率上, 也不妨花一点资源计算这个人类从来没有见过的伟大常数Q上, 至少计算到小数点后一亿位。根据我们的计算, 如果算到整数10的8次方, 这个常数Q的前6位都是由伟大的塞尔维亚科学家特斯拉预言的打开宇宙大门的关键钥匙的神秘数字3, 6, 9组成, 我们大胆猜测, 如果算到整数10的80次方那么这个常数Q的前60位；算到整数10的800次方那么这个常数Q的前600位；算到整数10的80000次方那么这个常数Q的前60000位都应该全部由3, 6, 9组成。如果算到整数10的8万亿次方, 那么这个常数Q的前6万亿位都应该全部由3, 6, 9组成。我们预测大常数Q的终极结果完全由0, 3, 6, 9这几个神秘数字组成。或许这个无穷大大数域的超级常数Q比传统普通数学常数圆周率还要重要还要深刻还要影响深远, 或许大常数Q可以揭示某些我们前所未见的更深刻的宇宙规律, 甚至大常数Q可以改变人类文明的走向呢！要知道大常数Q是浩瀚宇宙里微乎其微的一粒灰尘的蓝色星球上人这个卑微的无以复加的渺小物种在微不足道短暂的人类历史上用肉眼和细胞蛋白大脑外加一些原始粗糙的计算工具发现的第一个无穷大大系统之间的常数, 而和e等60多个数学常数都是普通常数, 不是无穷大大系统常数。

连续统假设是一个伪命题的论调可以休矣。

试想一下,如果一个数, 从头开始一直延伸到无穷无尽的无穷大, 一直延伸到无边无际浩瀚宇宙的深处, 全部是由神秘数字0, 3, 6, 9组成, 这个数将会是多么慑人魂魄, 多么宏伟壮观啊！这个壮丽辉煌的数里面会蕴藏多少宇宙的奥秘呢？这个数就炎黄子孙发现的气贯长虹的无穷大大常数Q！

在验证大常数Q的10^7, 10^8的激动人心的日子里, 为中华民族抢占人类智商的制高点, 为人类抢占未来数学的先机是作者当时激励所有参加计算验证人员的一句经典格言。

最后套用一句爱因斯坦数学老师闵可夫斯基的著名句型：能生在发现无穷大大常数Q和无穷大大数域的伟大时代, 能站在古往今来所有天才的肩上, 能利用现代文明最辉煌的成果作出新的发现, 能够抢先一窥浩瀚宇宙的伟大奥秘, 先睹为快, 千载难逢, 何其荣幸!

仅以此书抛砖引玉,希望全世界更多热爱科学热爱数学的勇士站在大数域理论的肩上作出更加伟大的发现。

十二、附录

附录1和附录2是美国美国纽约远见出版社威廉。丽萨等有关专家和专业作家们阅读《大数域原理》后写的书评和博文,比较全面公正的介绍了他们对《大数域原理》一书的理解, 专业素养深厚, 学识渊博, 文笔优美洗练, 旁征博引, 引经据典, 鲜活灵动, 简洁深刻, 评论常常一针见血且极富启发性, 让人不禁浮想联翩, 完全以第三方独立公正的立场看待大数域理论, 尤其是附录1的前五篇, 均在2023年的十月和十二月发表在纽约时报先锋周刊。作者觉得这些书评和博文不失为科普的好材料, 可以帮助读者从不同的视角理解《大数域原理》这个全新的数学理论, 特作为附录1和附录2附在文章结尾。

附录1和附录2见帖文《未来数学百科全书》和《深入宇宙的挂毯——探索无穷大领域》。

附录3是《大数域原理》英文版封面,网址和介绍。

附录4是《大数域原理》中文版封面,网址和介绍。